Tag: Ciekawostka

Matematyka w architekturze i tajemnicza złota proporcja

Budynki pełnią mnóstwo funkcji: dają nam schronienie przed ciepłem lub zimnem, możemy wewnątrz nich spać, gotować, uczymy się lub pracujemy 🙂. Jeżdżąc na wycieczki, podziwiamy przeróżne budowle, zachwycamy tym, jak są zbudowane i przemyślane. Projektowanie tego wszystkiego niestety nie jest tak proste, jakie się wydaje, gdy gramy w Simsy 😳. To, aby budynki były nie tylko ładne, ale też funkcjonalne i bezpieczne, jest pracą architektów. Zobacz, jak ważna jest w tym zawodzie matematyka oraz czym jest złota proporcja!

Obraz Francis z Pixabay

Jakie dziedziny matematyki są najbardziej przydatne?

Na pierwszym miejscu wobec najważniejszych dla architekta działów matematyki będzie geometria. 📐 Do zaprojektowania budynku potrzeba wiedzieć, na jakim obszarze będzie się on znajdował, jak powinien wyglądać jego kształt oraz jak duży ma być. Aby stworzyć projekt, który będzie mógł wejść w życie, architekt musi wyznaczyć odpowiednie proporcje, zrozumieć łączenie kształtów i relacje między różnymi elementami konstrukcji. Geometria jest też istotna przy konstruowaniu budynku, ponieważ określa siły, jakie działają na poszczególne ściany i elementy. Od ich rozkładu zależy to, czy koniec końców taka budowla nie zawali się pod swoim własnym ciężarem!

Obraz Andrzej z Pixabay

Kolejną bardzo ważną dziedziną w architekturze jest trygonometria. Projektanci budynków często muszą dokładnie znać teren, na jakim ma planuje się budowę. Ta dziedzina matematyki pomaga im dopasować odległości, wysokości i kąty terenu, aby projekt mógł powstać w danych warunkach terenowych. Dzięki niej określa się także kąt, pod jakim powinien być nachylony dach oraz rozmieszcza się okna i drzwi. Trygonometria pomaga też sprawdzić, jak światło wpadające przez okna będzie oświetlało daną przestrzeń!

Obraz Pexels z Pixabay

Architekt w oparciu o swoją wiedzę, tworzy mnóstwo rysunków technicznych 🖌, na których widnieją przekroje, proporcje, rzuty oraz odległości, jakie powinny mieć poszczególne części budynku. Jego projekty muszą być dopracowane co do najmniejszego szczegółu i przemyślane pod wieloma kątami.

Obraz 3844328 z Pixabay

Bryły, jakie nas otaczają

Skoro wiemy już, jak ważna jest w architekturze matematyka, zajmijmy się ukrytymi w niektórych znanych budowlach tajemnicami. 😀

Z niektórych łatwo zdać sobie sprawę, kiedy tylko pomyślimy, patrząc na niektóre dzieła architektoniczne. Na przestrzeni wieków często używano figur geometrycznych. Wieże tworzono jako walce, domy 🏠 to zazwyczaj prostopadłościany, a piramidy to ostrosłupy!

Obraz Simon z Pixabay

Obraz AI Leino z Pixabay

Inną łatwo zauważalną właściwością jest symetria. Dzięki niej czujemy satysfakcję, kiedy patrzymy na jakiś budynek. Dobrymi przykładami będą katedra Notre Dame oraz wiedeński Belweder:

Obraz Leif Linding z Pixabay

Obraz Anemone123 z Pixabay

Jednak w niektórych budowlach architektoniczne szczegóły są bardziej ukryte. Przykładem tego jest złota proporcja, czyli stosunek dwóch liczb do siebie, wynoszący około 1,618. Słysząc o tym po raz pierwszy, nie brzmi jakkolwiek ciekawie, jednak jeśli zagłębi się w temat, zdziwisz się, gdzie można ją spotkać! W architekturze złota proporcja jest używana jako jedno z narzędzi do osiągnięcia równowagi, harmonii i estetyki w projektach. ⚖️

Co ma złoto do podziału odcinka?

Złota proporcja powstała poprzez podział odcinka na dwie części tak, aby stosunek długości dłuższej z nich do krótszej, był taki sam jak całego odcinka do części dłuższej.

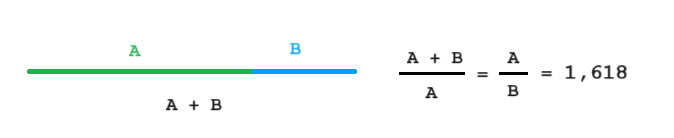
Wiemy już, że złota proporcja, nazywana też złotym podziałem, to po prostu poszukiwanie odpowiedniego punktu na odcinku, aby w wyniku dzielenia dostać liczbę phi – ϕ. Jej dokładna wartość wynosi tyle:

Zastanówmy się jednak, czy można podzielić tak odcinek w prosty sposób 🤔. Jest taka metoda i opiera się na ciągu Fibonacciego, czyli ciągu liczb, który powstaje z dodanie dwóch jego kolejnych elementów do siebie, aby otrzymać następny. Dwie pierwsze liczby to 1, trzecią więc jest 1+1=2, czwartą 1+2=3, piątą 3+2=5, szóstą 5+3+8 i tak dalej. Okazuje się, że w tym ciągu stosunek mniejszej liczby do kolejnej większej daje zbliżony wynik do 1,6180! 😮

Rysując kwadraty o długościach boków równych kolejnym elementom ciągu Fibonacciego, w prosty sposób uzyskamy złoty prostokąt.

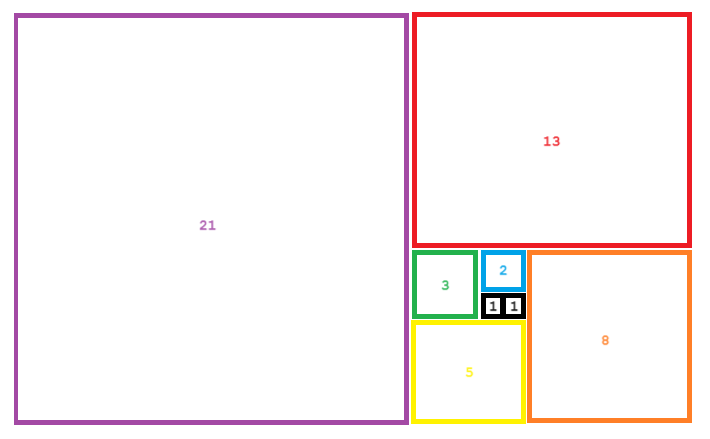
Złota spirala zachodzi, kiedy do złotego prostokąta, od jego najmniejszego elementu wpiszemy koła łączące się z sobą.

Złoty podział jest o tyle niesamowity, że patrząc na niego czujemy spokój, harmonię oraz równowagę 🤗. Bardziej skupiamy się na obrazie, który zachowuje takie, a nie inne proporcje. Wielu znamienitych artystów, a nawet Matka Natura, bardzo często korzystali z tej ciekawej właściwości!

Czas na przykłady

Nie widzimy tego na pierwszy rzut oka, ale w przyrodzie często spotykamy się ze złotą proporcją. Świetnym przykładem jest kształt nasion słonecznika, a nawet nasza galaktyka!

http://lambda.ckziu.jaworzno.pl/wp-content/uploads/2019/03/15.jpg

http://lambda.ckziu.jaworzno.pl/wp-content/uploads/2019/03/18.jpg

Skoro była mowa o architekturze, zauważ, że złoty podział zastosowano przy budowie greckiego Partenonu!

http://lambda.ckziu.jaworzno.pl/2019/03/28/zloty-podzial-czym-jest-i-gdzie-go-znajdziemy/

Bardzo polecam zapoznać się z większą ilością przykładów, a świetny film odnoszący się do liczby phi oraz złotego podziału jest tutaj. Jak widać, świat, architektura oraz matematyka mają przed nami mnóstwo tajemnic, które tylko czekają na odkrycie 😍! Na deser możesz jeszcze sprawdzić, jaka liczba wyjdzie, kiedy podzielisz swój wzrost przez odległość stóp do pępka albo odległość od końca palców do łokcia przez odległość od nadgarstka do łokcia! 😉

2024-05-02
Pszczółka Maja i jej kuzyni – czy pszczoły potrafią liczyć?
Mówi się, że w wigilię zwierzęta mówią ludzkim głosem. A co jeżeli możemy porozumiewać się z nimi na co dzień? Chociaż nie mają strun głosowych, jesteśmy w stanie znaleźć nić porozumienia ze zwierzakami – choćby w postaci wydawania komend naszym psiakom. Może i nie są w stanie odpowiedzieć, ale reagują na to, co mówimy, w wyuczony sposób. To jednak nie to samo, co liczenie, bo z tym wśród zwierzaków spotykamy się rzadko. Nawet mimo tego, że psy są inteligentne. Co dopiero z innymi, mniejszymi stworzeniami! A co, gdyby tak wziąć pszczoły – małe, pożyteczne owady, dzięki którym mamy owoce i warzywa? Czy w ich przypadku można w ogóle mówić o inteligencji? Okazuje się, że tak!

Obraz smellypumpy z Pixabay

Mózg o wadze 1 miligrama 🧠

Tak dla porównania – mózgi psów, zależnie od wielkości, mają od 50 do około 100 gramów¹. Ludzki mniej więcej 1,5 kilograma. Patrząc na te ogromne różnice, nikt nie spodziewałby się po bohaterach tego artykułu nadzwyczajnych wyników w nauce. A jednak wśród pszczół udało się zaobserwować złożone zachowania świadczące o ich niezwykłej bystrości i organizacji²:
- Pszczoły rozpoznają otoczenie, w jakim się znajdują i wybierają zawsze najkrótszą drogę do celu 🧭
- Te owady potrafią komunikować sobie nawzajem informacje o znalezionym pożywieniu wykonując „powietrzny taniec” 💭 👋
- Wykazują różne cechy – jedne są bardziej odważne niż inne, a także każda pszczoła może woleć trochę inne kwiaty 🌺
- Podczas opiekowania się młodymi, pszczoły potrafią sprawdzać je nawet 1300 razy na dobę 🐝
Obraz Akbar Nemati z Pixabay

Jak nauczyć pszczoły liczyć?

Skoro wiemy już, że te owady są znacznie bardziej złożone, niż się wydają, to przejdźmy do sedna tematu. Fakt, iż jakieś stworzenia potrafią nauczyć się rzeczy A nie znaczy że z rzeczą B pójdzie tak samo łatwo, a przecież posiadanie umiejętności nawigowania wcale nie leży blisko zdolności matematycznych! Jak zatem naukowcy podeszli do sprawy³?

Skoro wiemy już, że te owady są znacznie bardziej złożone, niż się wydają, to przejdźmy do sedna tematu. Fakt, iż jakieś stworzenia potrafią nauczyć się rzeczy A nie znaczy że z rzeczą B pójdzie tak samo łatwo, a przecież posiadanie umiejętności nawigowania wcale nie leży blisko zdolności matematycznych! Jak zatem naukowcy podeszli do sprawy?

Zdjęcie dodane przez Magda Ehlers: https://www.pexels.com/pl-pl/zdjecie/czerwone-tlo-z-123456789-nakladka-tekstu-1329296/

Pszczoły umieszczano w labiryncie o kształcie „Y”, gdzie uczono je liczyć. Przykładowo, najpierw wchodziły do pomieszczenia z numerem, na przykład „2”, a później musiały wybrać między dwoma pomieszczeniami – jednym z narysowanymi dwoma gwiazdkami a drugim z pięcioma. Jeżeli wybrały dobrze, dostawały nagrodę w postaci słodkiego syropu. Część pszczół była uczona odwrotnie – kojarzenia ilości z liczbami, przykładowo musiały wybrać spośród dwóch pudełek z tą samą liczbą przedmiotów, ale jedno pudełko było oznaczone złym numerem. Grupa, której wcześniej w ogóle nie uczono w labiryncie, kompletnie nie radziła sobie z żadnym z tych zadań.

Co ciekawe, jeżeli dane pszczoły nauczyły się łączyć numer z liczbą przedmiotów, nie rozumiały połączenia odwrotnego i nie umiały dopasować liczby przedmiotów do numeru. Pokazuje to, że mimo niektórych niezwykłych umiejętności pszczoły nie powalają inteligencją, ale z pewnością ta ciekawostka pozwoli uznać je za jeszcze bardziej fascynujące niż dotychczas!

Zdjęcie dodane przez Pew Nguyen: https://www.pexels.com/pl-pl/zdjecie/pszczoly-miod-pszczola-pracowita-pszczolka-7860749/

A co na to odkrycie amerykańscy naukowcy? 🤔

Dzięki badaniom nad zdolnościami matematycznymi pszczół badacze zainteresowali się mechanizmami, jakimi kieruje się pszczeli umysł. Fakt, że te malutkie owady nauczyły się nawet pojmowania zera, nie przeszedł w świecie nauki bez echa! Okazało się, że zapamiętywanie i rozpoznawanie liczby przedmiotów wymaga bardzo niewielkich zasobów mózgu. Zdaniem naukowców, wystarczą ZALEDWIE 4 NEURONY, aby móc to robić na najbardziej podstawowym poziomie⁴. Jak widać, duża głowa to nie wszystko!

Uzyskane wyniki mogą posłużyć do badań nad rozwojem sztucznej inteligencji, która dzięki technice uczenia pszczół będzie trenowana łatwiej oraz na znacznie prostych algorytmach. Dlatego dbajmy o pszczoły, bo są niesamowicie pożyteczne i nie wiadomo, czym jeszcze mogą nas zaskoczyć!
2023-05-25
Zachowanie mrówki, które pokonało matematyków!

Pamiętam, jak w dzieciństwie nie mogłam oderwać oczu od scen w filmach, gdzie występowali jacyś „hakerzy”. Za pomocą kilku komend potrafili przechytrzyć doświadczonych specjalistów, a ich zdolności logicznego myślenia oraz działania mimo stresu torowały im drogę przez wszystkie przeszkody. Później, w miarę nauki, dowiedziałam się, że hakerstwo wcale nie wygląda tak jak w filmach. Do tego wspomniane umiejętności są użyteczne nie tylko pracując przy komputerze, ale także w życiu.

Bystry umysł, duża wiedza i kreatywność to bezcenne umiejętności, na których bazują wszystkie zawody mające coś niecoś wspólnego z matematyką i rozwiązywaniem problemów. Aby je w sobie wykształcić, potrzeba lat cierpliwego zdobywania wiedzy, robienia zadań, rozwijania się oraz szukania nieszablonowych rozwiązań.

Obraz Ronny Overhate z Pixabay

Wszystko pięknie, ale co ma z tym wspólnego jakaś mrówka?

W roku 1986 amerykański informatyk Christofer Langton napisał pozornie prosty program. Symulował on ogromną kartkę papieru w kratkę, na którym stoi mrówka.
1. Jeżeli nasz owad jest na białym polu, zamalowuje je na czarno i skręca w lewo przechodząc na kolejne pole.

2. Kiedy mrówka znajdzie się na polu zamalowanym, przywraca mu biały kolor i skręca w prawo.

Langton zaobserwował coś bardzo ciekawego. Na początku mrówka kręciła się po wirtualnej kartce bez wyraźnego ładu i sensu, ale po prawie 10 000 krokach z chaosu wyłonił się regularny wzór¹!

Mrówka po wykonaniu 11 669 kroków

Mrówka zaczęła tworzyć coś na kształt prostej drogi, zamiast tak jak do tej pory zachowywać się nieprzewidywalnie. Dziwne, lekko okrężne ruchy przerodziły się w przedłużającą się co 104 kroki „autostradę”. Nieskomplikowane zasady rządzące światem naszej mrówki, sprowadzają jej cyfrowe życie do tworzenia prostych, symetrycznych wzorów.

Każda sprawdzona do tej pory konfiguracja startowa algorytmu w końcu zaczynała kreślić prostą drogę. Zaczynając na białym polu czy na czarnym, z czystą planszą bądź z częścią pól już zamalowanych. Najciekawszy w tym wszystkim jest fakt, że NIKT jeszcze nie wykazał, że stanie się tak ZAWSZE, ale w każdym badanym dotąd przypadku mrówka Langtona początkowo kręci się bez widocznego ładu i wykonuje chaotyczne, okrężne ruchy i pewnym momencie postanawia wykreślić prostą drogę.

Istnieją bardziej rozszerzone wersje algorytmu mrówki. Gregg Turk i Jim Propp dodali więcej mrówek i kolorów². Niektórzy tworzyli plansze, które zamiast kratek mają przykładowo sześciokąty. Mimo niesamowitych obrazów, jakie wyłaniają się z tych wszystkich symulacji, od pewnego momentu mrówki nie tworzą dalszych obrazów, a obierają sobie ścieżkę, z której już nie zbaczają. Jak wyglądają inne warianty mrówki możecie sprawdzić tutaj.

Czy i my jesteśmy jak mrówka?

Jak to wszystko ma się do wstępu? Być może nijak. Lecz faktem jest, że chociaż na początku przygody z czymś nowym często wydaje się to nam obce, skomplikowane i nie do ogarnięcia, po pewnym czasie staje się zrozumiałe, logiczne i proste. Tego też możemy dopatrzyć się w pozornie nieprzewidywalnym ruchu, który wykonuje mrówka Langtona. Koniec końców wybiera jakiś kierunek, a później niestrudzenie zmierza w nim, aż nam nie znudzi się jej obserwowanie i zamkniemy okienko³. Bo nauka i rozwój może być zabawą⁴.

2023-03-27
Jak działa kalendarz?
Kalendarz – czy to w aplikacji, czy stojący na biurku, czy też w formie książeczki-planera, praktycznie zawsze jest gdzieś pod ręką. Jest bardzo wygodnym przedmiotem do ustalania spotkań, przypominajki o rzeczach do zrobienia lub nauczenia, a także fajnym gadżetem do zapisywania swoich wspomnień. Bez niego ciężko byłoby nam się dogadywać, bo chociaż pojęcia takie jak „jutro” czy „wczoraj” są dla nas naturalne, jak dogadać się w sprawie czegoś odległego w czasie? I skąd wzięła się popularność naszego, gregoriańskiego kalendarza?

Skąd kalendarz się wziął?

Kalendarz towarzyszy nam odkąd tylko stworzyliśmy pierwsze cywilizacje. Jakoś trzeba było zapisywać wydatki i ustalać daty. Sam rok wziął się z tego, że jest to czas zatoczenia pełnego obrotu Ziemi wokół Słońca. Dzień i noc wyznacza obrót Ziemi wokół własnej osi. Dlaczego jednak mamy tygodnie i miesiące? Miesiąc to czas pełnego cyklu Księżyca, a tydzień wziął się z biblijnych 7 dni, kiedy to Bóg stworzył świat. Inaczej było w starożytnym Rzymie, gdzie początkowo tydzień miał 8 dni, a miesięcy było jedynie cztery!

Obraz Karolina Grabowska z Pixabay

Rodem z nad Nilu

Pierwszym znanym nam kalendarzem był system z Egiptu i Babilonu z około XVI w. p.n.e. Opierały się one o pory, kiedy rzeki wylewały się z brzegów , co wiązało się ze zmianą pór roku. Dzielili oni rok na 12 miesięcy. Co ciekawe, 1 stycznia wyznacza nam nowy rok na cześć tego, że w Egipcie tego dnia konsulowie obejmowali nowe urzędy¹!

Obraz Peggychoucair z Pixabay

A po drugiej stronie świata

Kolejnym i znanym kalendarzem jest ten wynaleziony przez Majów prawdopodobnie w XV wieku. Dzielił on rok na 18 miesięcy po 20 dni z 5 dodatkowymi, świątecznymi dniami na koniec roku. Stworzono go w kamieniu o kształcie słupa, dzielącym czas na jednostki od doby aż do 25 230 lat! Podstawą czasu były dni oraz dwudziestokrotności i lata, a czas mierzono od ustalonego „dnia zero”. Majowie byli zafascynowani obserwacjami astronomicznymi, dzięki czemu w oparciu o ruchy gwiazd dokonywali bardzo dokładnych obliczeń².

Obraz Francesco Foti z Pixabay

Wiele wieków później i aż do teraz

Dziś najpowszechniejszy kalendarz to gregoriański – poprawiona przez papieża Grzegorza XIII wersja kalendarza juliańskiego z 1582 roku. Dzieli on czas na rok – obrót Ziemi wokół Słońca, 12 miesięcy – Księżyc przechodzi wszystkie fazy dwanaście razy w ciągu roku, i doby wyznaczone dniem i nocą. Co 4 lata mamy 366 zamiast 365 dni, ponieważ Ziemia nie jest prostopadła w stosunku do naszej gwiazdy, ale lekko nachylona. Przez to dni w roku mają różną długość. Dodatkowo, obrót planety wokół własnej osi u nas wynosi odrobinę mniej niż ustalone 24 godziny. Dlatego po zsumowaniu wszystkich dni zobaczymy, że Ziemia w ciągu roku zdąży wykonać obrót trochę więcej niż 365 raza! Po 4 latach uzbiera się z tego cały dzień, przez co mamy lata przestępne, co wprowadził właśnie Grzegorz XIII³.

Zdjęcie dodane przez Александар Цветановић: https://www.pexels.com/pl-pl/zdjecie/brazowy-drewniany-kalendarz-na-biurko-z-13-wrzesnia-1425099/

Samo słowo pochodzi od łacińskiego „caledae”, czyli pierwszy dzień po nowiu Księżyca

To, jak na przestrzeni wieków mierzono upływ czasu, jest fascynujące i czytając o różnych kalendarzach wymyślanych przez dalekie cywilizacje dowiadujemy się wielu ciekawostek! Jedną z nich może być określenie jaki jest dzień tygodnia na podstawie samej daty!

Co ciekawe, istnieje na to wzór matematyczny, zwany regułą Zellera.
```
D = d + [(13 * (m + 1)) / 5] + B + (B/4) + (A/4) - 2 * A
gdzie d to dzień miesiąca, m numer miesiąca, A dwie pierwsze cyfry roku, B dwie ostatnie cyfry roku
```
Żeby działać zgodnie z regułą, potrzebujemy wiedzieć jeszcze jedno, miesiące liczone są od marca, który liczymy jako 3, więc kolejnymi są kwiecień 4, maj 5, itd., ale styczeń to już 13, a luty 14. Przez to marzec traktujemy jako obecny rok, ale styczeń i luty to jeszcze rok mniej.

Sprawdzimy datę 14 stycznia 2023 roku.

d = 15, m=13 (bo liczymy, że rok zaczyna się od marca, a jego numerem jest 3), A = 20, B = 22

Jeśli podczas dzielenia wyjdą nam wartości po przecinku, bierzemy tylko część całkowitą.
```
Nasz wzór to zatem:
D = 15 + [(13 * (13 + 1)) / 5] + 22 + (22/4) + (20/4) - 2 * 20 = 15 + 36 + 22 + 5 + 5 - 40 = 43
```
Nasz wynik dzielimy przez 7 i bierzemy resztę z dzielenia. W tym wypadku 28 / 7 to 6 (bo 6 * 7 = 28) no i reszta 1 (bo 29 – 28 = 1). Reszta to dzień tygodnia liczony, że 0 jest sobotą. Skoro wyszła nam jedynka, oznacza to, że 15 stycznia 2023 jest niedzielą!

Gdyby we wzorze wynik był ujemny, szukamy wielokrotności 7 większej lub równej wynikowi bez znaku. Wtedy odejmujemy od tej wielokrotności nasze D i mamy dzień tygodnia!

Teraz najważniejsze, czyli czemu ten wzór działa?

Dzielenia i mnożenia to poprawki i przesunięcia od danego dnia 0. d przesuwa dni miesiąca, a dzielenie i mnożenie po samym B, to końcowa poprawka na rok przestępny, która w ostatnim dzieleniu w razie czego dodaje nam dzień. Centralna część opiera się na liczbie dni w ciągu roku w poszczególnych miesiącach. Ponieważ liczymy od marca, liczby dni to kolejno 31, 30, 31, 30, 31, 31, 30, 31, 30, 31, 31, 28/29. Cały czas powtarzamy 31, 30, a co 5 miesięcy mamy kolejne 31, więc dzielimy przez 5. W każdym takim pięciomiesięcznym okresie zostaje nam dodatkowo z pełnych 4 tygodni, czyli 28 dni, które są w każdym miesiącu, kolejno 3, 2, 3, 2, 3, czyli 13 dni. Stąd mnożenie przez 13. Ostateczne dzielenie przez 7 pozwala na odczytanie dnia tygodnia.
2023-01-24